Automatically Signing a Windows EXE with Azure Trusted Signing, dotnet sign, and GitHub Actions
 Mac Tahoe (in Beta as of the time of this writing) has this new feature called Edge Light that basically puts a bright picture of an Edge Light around your screen and basically uses the power of OLED to give you a virtual ring light. So I was like, why can't we also have nice things? I wrote (vibed, with GitHub Copilot and Claude Sonnet 4.5) a Windows Edge Light App (source code at https://github.com/shanselman/WindowsEdgeLight and you can get the latest release here https://github.com/shanselman/WindowsEdgeLight/releases or the app will check for new releases and autoupdate with Updatum).
Mac Tahoe (in Beta as of the time of this writing) has this new feature called Edge Light that basically puts a bright picture of an Edge Light around your screen and basically uses the power of OLED to give you a virtual ring light. So I was like, why can't we also have nice things? I wrote (vibed, with GitHub Copilot and Claude Sonnet 4.5) a Windows Edge Light App (source code at https://github.com/shanselman/WindowsEdgeLight and you can get the latest release here https://github.com/shanselman/WindowsEdgeLight/releases or the app will check for new releases and autoupdate with Updatum).
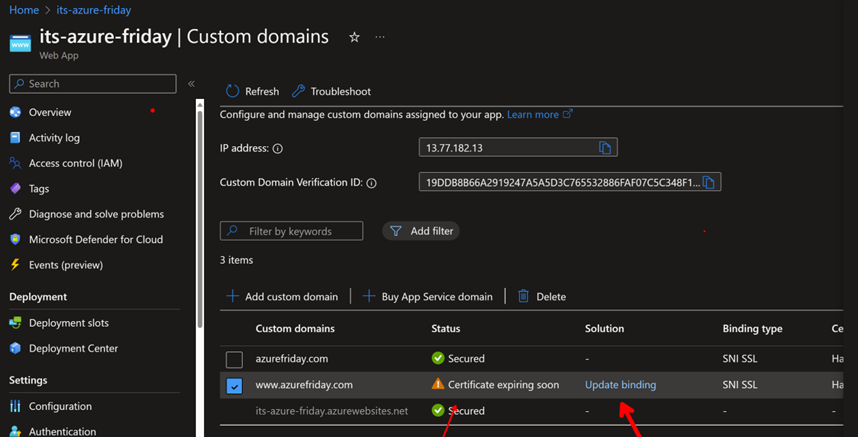
However, as is with all suss loose executables on the internet, when you run random stuff you'll often get the Window Defender 'new phone, who dis' warning which is scary. After several downloads and no viruses or complaints, my executable will eventually gain reputation with the Windows Defender Smart Screen service, but having a Code Signing Certificate is said to help with that. However, code signing certs are expensive and a hassle to manage and renew.
Someone told me that Azure Trusted Signing was somewhat less of a hassle - it's less, but it's still non-trivial. I read this post from Rick (his blog is gold and has been for years) earlier in the year and some of it was super useful and other stuff has been made simpler over time.
I wrote 80% of this blog post, but since I just spent an hour getting code signing to work and GitHub Copilot was going through and logging everything I did, I did use Claude 4.5 to help organize some of this. I have reviewed it all and re-written parts I didn't like, so any mistakes are mine.
Azure Trusted Signing is Microsoft's cloud-based code signing service that:
- No hardware tokens - Everything happens in the cloud
- Automatic certificate management - Certificates are issued and renewed automatically
- GitHub Actions integration - Sign during your CI/CD pipeline. I used GH Actions.
- Kinda Affortable - About $10/month for small projects. I would like it if this were $10 a year. This is cheaper than a yearly cert, but it'll add up after a while so I'm always looking for cheaper/easier options.
- Trusted by Windows - Uses the same certificate authority as Microsoft's own apps, so you should get your EXE trusted faster
Prerequisites
Before starting, you'll need:
- Azure subscription
- Azure CLI - Install from here
- Identity validation documents - Driver's license or passport for individual developers. Note that I'm in the US, so your mileage may vary but I basically set up the account, scanned a QR code, took a picture of my license, then did a selfie, then waited.
- Windows PC - For local signing (optional) but I ended up using the dotnet sign tool. There are
- GitHub repository - For automated signing (optional)
Part 1: Setting Up Azure Trusted Signing
Step 1: Register the Resource Provider
First, I need to enable the Azure Trusted Signing service in my subscription. This can be done in the Portal, or at the CLI.
# Login to Azure
az login
# Register the Microsoft.CodeSigning resource provider
az provider register --namespace Microsoft.CodeSigning
# Wait for registration to complete (takes 2-3 minutes)
az provider show --namespace Microsoft.CodeSigning --query "registrationState"
Wait until the output shows "Registered".
Step 2: Create a Trusted Signing Account
Now create the actual signing account. You can do this via Azure Portal or CLI.
Option A: Azure Portal (Easier for first-timers)
- Go to Azure Portal
- Search for "Trusted Signing Accounts"
- Click Create
- Fill in:
- Subscription: Your subscription
- Resource Group: Create new or use existing (e.g., "MyAppSigning")
- Account Name: A unique name (e.g., "myapp-signing")
- Region: Choose closest to you (e.g., "West US 2")
- SKU: Basic (sufficient for most apps)
- Click Review + Create, then Create
Option B: Azure CLI (Faster if you are a CLI person or like to drive stick shift)
# Create a resource group
az group create --name MyAppSigning --location westus2
# Create the Trusted Signing account
az trustedsigning create \
--resource-group MyAppSigning \
--account-name myapp-signing \
--location westus2 \
--sku-name Basic
Important: Note your region endpoint. Common ones are:
- East US:
https://eus.codesigning.azure.net/ - West US 2:
https://wus2.codesigning.azure.net/ - Your specific region: Check in Azure Portal under your account's Overview page
I totally flaked on this and messed around for 10 min before I realized that this URL matters and is specific to your account. Remember this endpoint.
Step 3: Complete Identity Validation
This is the most important step. Microsoft needs to verify you're a real person/organization.
- In Azure Portal, go to your Trusted Signing Account
- Click Identity validation in the left menu
- Click Add identity validation
- Choose validation type:
- Individual: For solo developers (uses driver's license/passport)
- Organization: For companies (uses business registration documents)
- For Individual validation:
- Upload a clear photo of your government-issued ID
- Provide your full legal name (must match ID exactly)
- Provide your email address
- Submit and wait for approval
Approval Time:
- Individual: Usually 1-3 business days
- Organization: 3-5 business days
- Me: This took about 4 hours, so again, YMMV. I used my personal account and my personal Azure (don't trust MSFT folks with unlimited Azure credits, I pay for my own) so they didn't know it was me. I went through the regular line, not the Pre-check line LOL.
You'll receive an email when approved. You cannot sign any code until this is approved.
Step 4: Create a Certificate Profile
Once your identity is validated, create a certificate profile. This is what actually issues the signing certificates.
- In your Trusted Signing Account, click Certificate profiles
- Click Add certificate profile
- Fill in:
- Profile name: Descriptive name (e.g., "MyAppProfile")
- Profile type: Choose Public Trust (required to prevent SmartScreen)
- Identity validation: Select your approved identity
- Certificate type: Code Signing
- Click Add
Important: Only "Public Trust" profiles prevent SmartScreen warnings. "Private Trust" is for internal apps only. This took me a second to realize also as it's not an intuitive name.
Step 5: Verify Your Setup
# List your Trusted Signing accounts
az trustedsigning show \
--resource-group MyAppSigning \
--account-name myapp-signing
# Should show status: "Succeeded"
Write down these values - you'll need them later:
- Account Name:
myapp-signing - Certificate Profile Name:
MyAppProfile - Endpoint URL:
https://wus2.codesigning.azure.net/(or your region) - Subscription ID: Found in Azure Portal
- Resource Group:
MyAppSigning
Part 2: Local Code Signing
Now let's sign an executable on your my machine. You don't NEED to do this, but I wanted to try it locally to avoid a bunch of CI/CD runs, and I wanted to right-click the EXE and see the cert in Properties before I took it all to the cloud. The nice part about this was that I didn't need to mess with any certificates.
Step 1: Assign Yourself the Signing Role
You need permission to actually use the signing service.
Option A: Azure Portal
- Go to your Trusted Signing Account
- Click Access control (IAM)
- Click Add → Add role assignment
- Search for and select Trusted Signing Certificate Profile Signer. This is important. I searched for "code" and found nothing. Search for "Trusted"
- Click Next
- Click Select members and find your user account
- Click Select, then Review + assign
Option B: Azure CLI
# Get your user object ID
$userId = az ad signed-in-user show --query id -o tsv
# Assign the role
az role assignment create \
--role "Trusted Signing Certificate Profile Signer" \
--assignee-object-id $userId \
--scope /subscriptions/YOUR_SUBSCRIPTION_ID/resourceGroups/MyAppSigning/providers/Microsoft.CodeSigning/codeSigningAccounts/myapp-signing
Replace YOUR_SUBSCRIPTION_ID with your actual subscription ID.
Step 2: Login with the Correct Scope
This is crucial - you need to login with the specific codesigning scope.
# Logout first to clear old tokens
az logout
# Login with codesigning scope
az login --use-device-code --scope "https://codesigning.azure.net/.default"
This will give you a code to enter at https://microsoft.com/devicelogin. Follow the prompts.
Why device code flow? Because Azure CLI's default authentication can conflict with Visual Studio credentials in my experience. Device code flow is more reliable for code signing.
Step 3: Download the Sign Tool
Option A: Install Globally (Recommended for regular use)
# Install as a global tool (available everywhere)
dotnet tool install --global --prerelease sign
# Verify installation
sign --version
Option B: Install Locally (Project-specific)
# Install to current directory
dotnet tool install --tool-path . --prerelease sign
# Use with .\sign.exe
Which should I use?
- Global: If you'll sign multiple projects or sign frequently
- Local: If you want to keep the tool with a specific project or don't want it in your PATH
Step 4: Sign Your Executable
Note again that code signing URL is specific to you. The tscp is your Trusted Signing Certificate Profile name and the tsa is your Trusted Signing Account name. I set *.exe to sign all the EXEs in the folder and note that the -b base directory is an absolute path, not a relative one. For me it was d:\github\WindowsEdgeLight\publish, and your mileage will vary.
# Navigate to your project folder
cd C:\MyProject
# Sign the executable
.\sign.exe code trusted-signing `
-b "C:\MyProject\publish" `
-tse "https://wus2.codesigning.azure.net" `
-tscp "MyAppProfile" `
-tsa "myapp-signing" `
*.exe `
-v Information
Parameters explained:
-b: Base directory containing files to sign-tse: Trusted Signing endpoint (your region)-tscp: Certificate profile name-tsa: Trusted Signing account name*.exe: Pattern to match files to sign-v: Verbosity level (Trace, Information, Warning, Error)
Expected output:
info: Signing WindowsEdgeLight.exe succeeded.
Completed in 2743 ms.
Step 5: Verify the Signature
You can do this in PowerShell:
# Check the signature
Get-AuthenticodeSignature ".\publish\MyApp.exe" | Format-List
# Look for:
# Status: Valid
# SignerCertificate: CN=Your Name, O=Your Name, ...
# TimeStamperCertificate: Should be present
Right-click the EXE → Properties → Digital Signatures tab:
- You should see your signature
- "This digital signature is OK"
Common Local Signing Issues
I hit all of these lol
Issue: "Please run 'az login' to set up account"
- Cause: Not logged in with the right scope
- Fix: Run
az logoutthenaz login --use-device-code --scope "https://codesigning.azure.net/.default"
Issue: "403 Forbidden"
- Cause: Wrong endpoint, account name, or missing permissions
- Fix:
- Verify endpoint matches your region (wus2, eus, etc.)
- Verify account name is exact (case-sensitive)
- Verify you have "Trusted Signing Certificate Profile Signer" role
Issue: "User account does not exist in tenant"
- Cause: Azure CLI trying to use Visual Studio credentials
- Fix: Use device code flow (see Step 2)
Part 3: Automated Signing with GitHub Actions
This is where the magic happens. I want to automatically sign every release. I'm using GitVersion so I just need to tag a commit and GitHub Actions will kick off a run. You can go look at a real run in detail at https://github.com/shanselman/WindowsEdgeLight/actions/runs/19775054123
Step 1: Create a Service Principal
GitHub Actions needs its own identity to sign code. We'll create a service principal (like a robot account). This is VERY different than your local signing setup.
Important: You need Owner or User Access Administrator role on your subscription to do this. If you don't have it, ask your Azure admin or a friend.
# Create service principal with signing permissions
az ad sp create-for-rbac \
--name "MyAppGitHubActions" \
--role "Trusted Signing Certificate Profile Signer" \
--scopes /subscriptions/YOUR_SUBSCRIPTION_ID/resourceGroups/MyAppSigning/providers/Microsoft.CodeSigning/codeSigningAccounts/myapp-signing \
--json-auth
This outputs JSON like this:
{
"clientId": "12345678-1234-1234-1234-123456789abc",
"clientSecret": "super-secret-value-abc123",
"tenantId": "87654321-4321-4321-4321-cba987654321",
"subscriptionId": "abcdef12-3456-7890-abcd-ef1234567890"
}
SAVE THESE VALUES IMMEDIATELY! You can't retrieve the clientSecret again. This is super important.
Alternative: Azure Portal Method
If CLI doesn't work:
- Azure Portal → App registrations → New registration
- Name: "MyAppGitHubActions"
- Click Register
- Copy the Application (client) ID - this is
AZURE_CLIENT_ID - Copy the Directory (tenant) ID - this is
AZURE_TENANT_ID - Go to Certificates & secrets → New client secret
- Description: "GitHub Actions"
- Expiration: 24 months (max)
- Click Add and immediately copy the Value - this is
AZURE_CLIENT_SECRET - Go to your Trusted Signing Account → Access control (IAM)
- Add role assignment → Trusted Signing Certificate Profile Signer
- Select members → Search for "MyAppGitHubActions"
- Review + assign
Step 2: Add GitHub Secrets
Go to your GitHub repository:
- Settings → Secrets and variables → Actions
- Click New repository secret for each:
AZURE_CLIENT_ID- From service principal output or App registrationAZURE_CLIENT_SECRET -From service principal output or Certificates & secretsAZURE_TENANT_ID- From service principal output or App registrationAZURE_SUBSCRIPTION_ID- Azure Portal → Subscriptions
Security Note: These secrets are encrypted and never visible in logs. Only your workflow can access them. You'll never see them again.
Step 3: Update Your GitHub Workflow
This is a little confusing as it's YAML, which is Satan's markup, but it's what we have sunk to as a society.
Note the dotnet-version below. Yours might be 8 or 9, etc. Also, I am building both x64 and ARM versions and I am using GitVersion so if you want a more complete build.yml, you can go here https://github.com/shanselman/WindowsEdgeLight/blob/master/.github/workflows/build.yml I am also zipping mine up and prepping my releases so my loose EXE lives in a ZIP file.
Add signing steps to your .github/workflows/build.yml:
name: Build and Sign
on:
push:
tags:
- 'v*'
workflow_dispatch:
permissions:
contents: write
jobs:
build:
runs-on: windows-latest
steps:
- name: Checkout code
uses: actions/checkout@v4
with:
fetch-depth: 0
- name: Setup .NET
uses: actions/setup-dotnet@v4
with:
dotnet-version: '10.0.x'
- name: Restore dependencies
run: dotnet restore MyApp/MyApp.csproj
- name: Build
run: |
dotnet publish MyApp/MyApp.csproj `
-c Release `
-r win-x64 `
--self-contained
# === SIGNING STEPS START HERE ===
- name: Azure Login
uses: azure/login@v2
with:
creds: '{"clientId":"${{ secrets.AZURE_CLIENT_ID }}","clientSecret":"${{ secrets.AZURE_CLIENT_SECRET }}","subscriptionId":"${{ secrets.AZURE_SUBSCRIPTION_ID }}","tenantId":"${{ secrets.AZURE_TENANT_ID }}"}'
- name: Sign executables with Trusted Signing
uses: azure/trusted-signing-action@v0
with:
azure-tenant-id: ${{ secrets.AZURE_TENANT_ID }}
azure-client-id: ${{ secrets.AZURE_CLIENT_ID }}
azure-client-secret: ${{ secrets.AZURE_CLIENT_SECRET }}
endpoint: https://wus2.codesigning.azure.net/
trusted-signing-account-name: myapp-signing
certificate-profile-name: MyAppProfile
files-folder: ${{ github.workspace }}\MyApp\bin\Release\net10.0-windows\win-x64\publish
files-folder-filter: exe
files-folder-recurse: true
file-digest: SHA256
timestamp-rfc3161: http://timestamp.acs.microsoft.com
timestamp-digest: SHA256
# === SIGNING STEPS END HERE ===
- name: Create Release
if: startsWith(github.ref, 'refs/tags/')
uses: softprops/action-gh-release@v2
with:
files: MyApp/bin/Release/net10.0-windows/win-x64/publish/MyApp.exe
env:
GITHUB_TOKEN: ${{ secrets.GITHUB_TOKEN }}
Key points:
endpoint: Use YOUR region's endpoint (wus2, eus, etc.)trusted-signing-account-name: Your account name (exact, case-sensitive)certificate-profile-name: Your certificate profile name (exact, case-sensitive)files-folder: Path to your compiled executablesfiles-folder-filter: File types to sign (exe, dll, etc.)files-folder-recurse: Sign files in subfolders
Step 4: Test the Workflow
Now trigger the workflow. You have two options:
Option A: Manual Trigger (Safest for testing)
Since the workflow includes workflow_dispatch:, you can trigger it manually without creating a tag:
# Trigger manually via GitHub CLI
gh workflow run build.yml
# Or go to GitHub web UI:
# Actions tab → "Build and Sign" workflow → "Run workflow" button
This is ideal for testing because:
- No tag required
- Won't create a release
- Can test multiple times
- Easy to debug issues
Option B: Create a Tag (For actual releases)
# Make sure you're on your main branch with no uncommitted changes
git status
# Create and push a tag
git tag v1.0.0
git push origin v1.0.0
Use this when you're ready to create an actual release with signed binaries. This is what I am doing on my side.
Step 5: Monitor the Build
Watch the progress with GitHub CLI:
# See latest runs
gh run list --limit 5
# Watch a specific run
gh run watch
# View detailed status
gh run view --log
Or visit: https://github.com/YOUR_USERNAME/YOUR_REPO/actions
Look for:
- Azure Login - Should complete in ~5 seconds
- Sign executables with Trusted Signing - Should complete in ~10-30 seconds
- Create Release - Your signed executable is now available in /releases in your GitHib project
Common GitHub Actions Issues
I hit a few of these, natch.
Issue: "403 Forbidden" during signing
- Cause: Service principal doesn't have permissions
- Fix:
- Go to Azure Portal → Trusted Signing Account → Access control (IAM)
- Verify "MyAppGitHubActions" has "Trusted Signing Certificate Profile Signer" role
- If not, add it manually
Issue: "No files matched the pattern"
- Cause: Wrong
files-folderpath or build artifacts in wrong location - Fix:
- Add a debug step before signing:
- run: Get-ChildItem -Recurse - Find where your EXE is actually located
- Update
files-folderto match
- Add a debug step before signing:
Issue: Secrets not working
- Cause: Typo in secret name or value not saved
- Fix:
- Verify secret names EXACTLY match (case-sensitive)
- Re-create secrets if unsure
- Make sure no extra spaces in values
Issue: "DefaultAzureCredential authentication failed"
- Cause: Usually wrong tenant ID or client ID
- Fix: Verify all 4 secrets are correct from service principal output
Part 4: Understanding the Certificate
Certificate Lifecycle
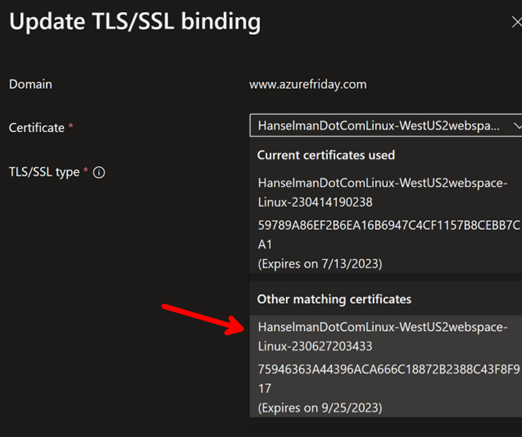
Azure Trusted Signing uses short-lived certificates (typically 3 days). This freaked me out but they say this is actually a security feature:
- If a certificate is compromised, it expires quickly
- You never manage certificate files or passwords
- Automatic renewal - you don't have to do anything
But won't my signature break after 3 days?
No, it seems that's what timestamping is for. When you sign a file:
- Azure issues a 3-day certificate
- The file is signed with that certificate
- A timestamp server records "this file was signed on DATE"
- Even after the certificate expires, the signature remains valid because the timestamp proves it was signed when the certificate was valid
That's why both local and GitHub Actions signing include:
timestamp-rfc3161: http://timestamp.acs.microsoft.com
What the Certificate Contains
Your signed executable has a certificate with:
- Subject: Your name (e.g., "CN=John Doe, O=John Doe, L=Seattle, S=Washington, C=US")
- Issuer: Microsoft ID Verified CS EOC CA 01
- Valid Dates: 3-day window
- Key Size: 3072-bit RSA (very secure)
- Enhanced Key Usage: Code Signing
Verify Certificate on Any Machine
# Using PowerShell
Get-AuthenticodeSignature "MyApp.exe" | Select-Object -ExpandProperty SignerCertificate | Format-List
# Using Windows UI
# Right-click EXE → Properties → Digital Signatures tab → Details → View Certificate
This whole thing took me about an hour to 75 minutes. It was detailed, but not deeply difficult. Misspellings, case-sensitivity, and a few account issues with Role-Based Access Control did slow me down. Hope this helps!
Used Resources
- Azure Trusted Signing Documentation
- dotnet/sign Tool
- azure/trusted-signing-action
- Windows Code Signing Best Practices
- SmartScreen Reputation System
Written in November 2025 based on real-world implementation for WindowsEdgeLight. Your setup might vary slightly depending on Azure region and account type. Things change, be stoic.
About Scott
Scott Hanselman is a former professor, former Chief Architect in finance, now speaker, consultant, father, diabetic, and Microsoft employee. He is a failed stand-up comic, a cornrower, and a book author.
About Newsletter

 See
See 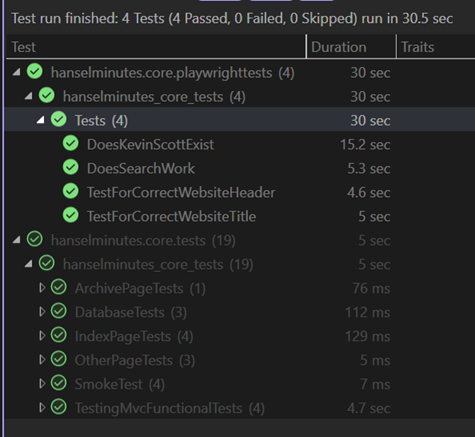 I've been doing not just Unit Testing for my sites but full on Integration Testing and Browser Automation Testing as early as 2007 with Selenium. Lately, however, I've been using the faster and generally more compatible
I've been doing not just Unit Testing for my sites but full on Integration Testing and Browser Automation Testing as early as 2007 with Selenium. Lately, however, I've been using the faster and generally more compatible